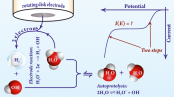
Full Model for the Two-Step Polarization Curves of Hydrogen Evolution, Measured on RDEs in Dilute Acid Solutions
The paper authored by
M. Gálvez-Vázquez, V. Grozovski,
N. Kovács, P. Broekmann and
S. Vesztergom
is published in Journal of Physical Chemistry C (2020, vol. 124, pp. 3988–4000).
Abstract:
Polarization curves of the hydrogen evolution reaction (HER), recorded on rotating disk electrodes (RDEs) in mildly acidic solutions, usually show a “two step” behavior. That is, two exponentially rising segments (the first commonly assigned to H+, the second to water reduction) are separated by a limiting current plateau. Here, we devise an analytical model for the full polarization curve by assuming that HER proceeds according to a quasireversible two-electron reaction, H+ + H2O + 2e– ⇌ H2 + OH–, obeying the Erdey-Grúz–Volmer–Butler equation. Our model is able to reproduce the two step behavior of polarization curves and can also be used for the fitting of measured currents over a broad range of pH, rotation rate, and electrode potential, on both Au and on Pt. We show that the length of the limiting current plateaus measured on RDEs for HER is inversely related to the electrocatalytic activity of the electrode and that at a given rotation rate a linear relationship exists between the plateau length and the bulk solution pH. By analyzing this relationship, we can estimate kinetic parameters, even in cases where the transport performance of the RDE would otherwise not be sufficient to measure well-defined kinetic currents at low overpotentials.
